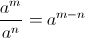Las leyes de los exponentes no es más que sumar multiplicar o dividir exponentes, solo necesitamos saber en que momento tenemos que hacer cada operación. Un exponente se puede definir como el número que define la cantidad de veces que se tiene qué multiplicar un factor por sí mismo, sencillo ¿verdad? el problema es cuando tenemos que elevar algo a la "cero" o manejar exponentes fraccionarios o incluso exponentes literales, las siguiente reglas serán de utilidad:
 |
$a^{\frac{m}{n}}=\sqrt[n]{a^{m}}$
De acuerdo con las reglas anteriores tenemos que todo número elevado a la "cero" es igual a la unidad, un factor elevado a la unidad da como resultado el mismo número, también que un exponente negativo indica que divide al factor que lo acompaña o que cuando multiplicamos factores con misma base debemos sumar los exponentes, etc. Expongamos pues cada caso usando ejemplos.
Potencias con exponente negativo
Al tener un exponente negativo debemos aplicar nuestra tercera regla de los exponentes, dividir nuestros factores por el factor con exponente negativo.
Multiplicación de potencias con misma base
Al multiplicar potencias con la misma base la ley de los exponentes nos dice que tenemos que sumarlo los exponentes.
No importa si el exponente es fraccionario o negativo, al multiplicar potencias con misma base es necesario sumarlos.
Publicidad
División de potencias con misma base
Cuando dividimos potencias donde su base es igual debemos restar los exponentes, al exponente del numerador restaremos el exponente del denominador.
Como se ve en los ejemplos al dividir las potencias con igual base se debe hacer una resta de los exponentes al exponente de "arriba" restaremos el de "abajo". En la siguiente entrada veremos las leyes de los exponentes cuando un exponente es elevado a una potencia y exponentes fraccionarios utilizando algunos ejercicios. Leyes Exponentes II
Ejercicios
$x^{-z}=$
$x^{m}x^{m}=$ Ver soluciones
$\frac{b^{2}}{b^{3}}=$