En la multiplicación de monomios por polinomios podemos establecer la siguiente regla:
Debemos multiplicar el monomio por cada término del polinomio haciendo caso a la ley de los signos y separando los productos resultantes con sus propios signos.
Siempre podemos comprender mejor viendo un ejemplo, hagamos pues la siguiente multiplicación:
Empecemos por efectuar cada multiplicación por separado esto es:
Ahora unamos los resultados parciales separados por su signo, quedando:
Debemos multiplicar el monomio por cada término del polinomio haciendo caso a la ley de los signos y separando los productos resultantes con sus propios signos.
Siempre podemos comprender mejor viendo un ejemplo, hagamos pues la siguiente multiplicación:
Empecemos por efectuar cada multiplicación por separado esto es:
Lo que vemos en este ejemplo no es más que la ley distributiva de la multiplicación aplicada, otra cosa interesante que observamos es que un producto puede representarse como una suma y que una suma a su vez puede condensarse en un producto, nada del otro mundo pero es muy útil acostumbrarnos a ver patrones en el álgebra, lo que después nos llevará a ver la factorización. Por lo pronto sigamos con otro ejemplo, multiplicar:
Empecemos por multiplicar el monomio por cada uno de los elementos del polinomio:
Solo juntamos los resultados y es nuestra solución:
Ejercicios












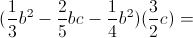

No hay comentarios.:
Publicar un comentario